PINE LIBRARY
Mis à jour FunctionBlackScholes
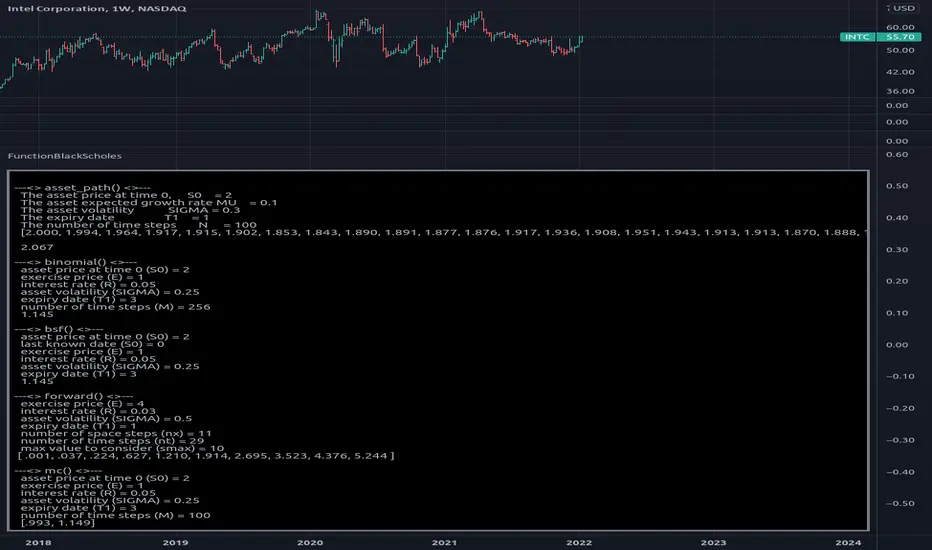
Library "FunctionBlackScholes"
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Some methods for the Black Scholes Options Model, which demonstrates several approaches to the valuation of a European call.
// reference:
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.html
// people.math.sc.edu/Burkardt/py_src/black_scholes/black_scholes.py
asset_path(s0, mu, sigma, t1, n) Simulates the behavior of an asset price over time.
Parameters:
s0: float, asset price at time 0.
mu: float, growth rate.
sigma: float, volatility.
t1: float, time to expiry date.
n: int, time steps to expiry date.
Returns: option values at each equal timed step (0 -> t1)
binomial(s0, e, r, sigma, t1, m) Uses the binomial method for a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: option value at time 0.
bsf(s0, t0, e, r, sigma, t1) Evaluates the Black-Scholes formula for a European call.
Parameters:
s0: float, asset price at time 0.
t0: float, time at which the price is known.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
Returns: option value at time 0.
forward(e, r, sigma, t1, nx, nt, smax) Forward difference method to value a European call option.
Parameters:
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
nx: int, number of space steps in interval (0, L).
nt: int, number of time steps.
smax: float, maximum value of S to consider.
Returns: option values for the european call, float array of size ((nx-1) * (nt+1)).
mc(s0, e, r, sigma, t1, m) Uses Monte Carlo valuation on a European call.
Parameters:
s0: float, asset price at time 0.
e: float, exercise price.
r: float, interest rate.
sigma: float, volatility.
t1: float, time to expiry date.
m: int, time steps to expiry date.
Returns: confidence interval for the estimated range of valuation.
Notes de version
v2 fixed some issues.Bibliothèque Pine
Dans l'esprit TradingView, l'auteur a publié ce code Pine sous forme de bibliothèque open source afin que d'autres programmeurs Pine de notre communauté puissent le réutiliser. Bravo à l'auteur! Vous pouvez utiliser cette bibliothèque à titre privé ou dans d'autres publications open source, mais la réutilisation de ce code dans des publications est régie par nos Règles.
Clause de non-responsabilité
Les informations et publications ne sont pas destinées à être, et ne constituent pas, des conseils ou recommandations financiers, d'investissement, de trading ou autres fournis ou approuvés par TradingView. Pour en savoir plus, consultez les Conditions d'utilisation.
Bibliothèque Pine
Dans l'esprit TradingView, l'auteur a publié ce code Pine sous forme de bibliothèque open source afin que d'autres programmeurs Pine de notre communauté puissent le réutiliser. Bravo à l'auteur! Vous pouvez utiliser cette bibliothèque à titre privé ou dans d'autres publications open source, mais la réutilisation de ce code dans des publications est régie par nos Règles.
Clause de non-responsabilité
Les informations et publications ne sont pas destinées à être, et ne constituent pas, des conseils ou recommandations financiers, d'investissement, de trading ou autres fournis ou approuvés par TradingView. Pour en savoir plus, consultez les Conditions d'utilisation.